Bashkësitë

Bashkësia është koncepti themelor i matematikës bashkohore. Bashkësia përbëhet nga objektet të cilat kanë së paku një veti të përbashkët. Objektet e bashkësisë i quajmë elemente të bashkësisë. Emërtimi dhe shënimi i bashkësive zakonisht bëhet me shkronja të mëdha të alfabetit latin. Caktimi i bashkësive bëhet në dy mënyra :

Duke i numëruar elementet e bashkësisë nëse numri i elementeve është i vogël si p.sh.: $A = (a 1, a 2, a 3,..., a n)$
Duke i përshkruar vetit e përbashkëta të elementeve si p.sh.: $A = {x | F (x)}$

Bashkësitë numerike

Bashkësia e numrave natyral: 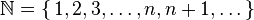$mathbb{N} = {, 1, 2, 3, ldots , n, n+1, ldots ,}$

Bashkësia e numrave të plotë: $mathbb{Z} = {, ldots , -2, -1, 0, 1, 2, 3, ldots , n, n+1, ldots ,}$

Bashkësia e numrave racional: $mathbb{Q} = left{frac{m}{n} | m in mathbb{Z}, n in mathbb{Z}, n ne 0 right}$

Bashkësia e numrave real: $mathbb{R} = { x|- infty <x<+ infty ,}$

Bashkësia e numrave kompleks: 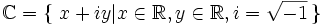$mathbb{C} = { x+iy|x inmathbb{R} ,y inmathbb{R} ,i= sqrt{-1} ,}$

Bashkësia e numrave çift: $mathbb{N_+} = { 2n|ninmathbb{N} land n vdots 2 ,}$ ={2,4,6,8,...}

Bashkësia e numrave tek: $mathbb{N_-} = { n|x inmathbb{N} land n notvdots 2 ,}$ ={1,3,5,7,9,...}

Veprimet me bashkësi

Prerja e bashkësive

Prerja e bashkësive $A$ dhe $B$ quhet bashkësia e cila i përmban elementet e $A$ dhe $B$

figura.

Unioni (apo bashkimi) i bashkësive

Unioni i bashkësive $A$ dhe $B$ quhet bashkësia e cila ka të gjitha elementet e bashkësive $A$ dhe $B$

figura. Për unionin e bashkësive vlejnë këto ligje :

Ligji i indempotencës

$Acup A=A$

Ligji i kumutativ

$Acup B=Bcup A$

Ligji asociativ

$A U (B U C) = (A U B) U C$

Ligji distribtiv

Ligji distribtiv

Diferenca e bashkësive

Diferenca e bashkësive $A$ dhe $B$ quhet bashkësia e cila ka vetëm elementet e bashkësisë $A$ që nuk i takojnë bashkësisë $B$

figura.

Diferenca simetrike e bashkësive

Diferenca simetrike e bashkësive $A$ dhe $B$ quhet bashkësia e cila ka vetëm elementet jo të përbashkëta të bashkësive $A$ dhe $B$

figura.

Relacionet

Relacionet binare

Nëse me $A$ shënojmë bashkësinë jo të zbrazët dhe me $ρ$ relacionin (raportin, marëdhëniet ) mes elemteve të $A$ -së, atëherë për $ρ$ themi se është relacion binar. Relacion binar quhet çdo nënbashkësi e katrorit kartezian : $A x B$
Vetit e relacionit binar janë:
Refleksiviteti Nëse në bashkësinë jo të zbrazët $A$ vlenë relacioni $ρ$ i cili ka vetitë $a ρ b$ dhe $b ρ a$ atëherë themi se kemi të bëjmë me relacionin binarë.

Në të kundërtën nëse vlen:

themi se kemi të bëjmë me relacion jorefleksiv.
Simetria Nëse në bashkësinë jo të zbrazët $A$ nga relacioni binar $ρ$ rrjedhë $b ρ a$ atëherë themi se kemi të bëjmë me relacion binarë simetrikë

Në të kundërtën nëse vlen:

themi se kemi të bëjmë me relacion asimetrikë.
Transitiviteti Nëse në bashkësinë jo të zbrazët $A$ nga relacionet binare $a ρ b$ dhe $b ρ a$ rrjedhë $a ρ c$ atëherë themi se kemi të bëjmë me relacion binar transitiv

Në të kundërtën nëse vlen:

themi se kemi të bëjmë me relacion intransitiv.

Relacioni i ekuivalencës

Relacioni i ekuivalencës është relacioni binarë $ρ$ i cili në bashkësinë $A$ është refleksiv, simetrik dhe transitiv. Simboli i relacionit të ekuivalencës është " 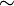$sim$ " .
Relacionet më të rëndësishme të ekuivalencës janë barazia, paralelshmëria, kongruenca dhe ngjashmëria. Po ashtu ekuacioni i ekuivalencës mundë të zbërthehet në klasa të ekuivalencës.

Relacioni i renditjes

Relacioni i renditjes është relacioni binarë $ρ$ i cili në bashkësinë $A$ është refleksiv, antisimetrik dhe transitiv.
Nëse relacioni i binarë $ρ$ në bashkësinë $A$ është irefleksivë, asimetrik dhe transitiv, atëherë themi se kemi të bëjmë me relacionin rigoroz ( të renditjes).

Relacionet ndërmjet dy bashkësive

Relacion ndërmjet dy bashkësive është prodhimi kartezian $A x B$ i bashkësive jo të zbrazëta $A$ dhe $B$ . Prodhimi kartezian është ç´do nënëbashkësi për të cilën vlen : $rho = left { (a,b)| a in A land b in B land a rho b right }$

Pasqyrimet

Pasqyrim (funksion, rifigurim ) i bashkësisë $A$ në $B$ quhet relacioni $ρ$ ndërmjet dy bashkësive $A$ dhe $B$ , i cili ka këtë veti :

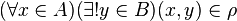
$( forall x in A)( exists !y in B)(x,y) in rho$

Elementet e bashkësisë $A$ që pasqyrohen në bashkësinë $B$ janë origjinal (zanafilla, fytyra) e pasqyrimi, ndërsa elementet përkatëse të bashkësisë $B$ që i shoqërohen origjinaleve quhen transformati (figura, përfytyrimi) i pasqyrimit. Pasqyrimet zakonisht nuk shënohen me $ρ$ por me $f, g, h,ψ$ etj. Shënimi i pasqyrimeve bëhet në disa mënyra varësisht nga lëmit në të cilën përdoret. Disa shembuj të shënimit të pasqyrimeve po i prezantojmë më poshtë.

Shënimi simbolik i pasqyrimit

$f: A to B$ ose $f: x to y =f(x) , forall x in A$

Shënimi i pasqyrimeve te bashkësitë e fundme (me simbole te Wik-it ende nuk mundem)
Shënimi i pasqyrimeve në formë tabelore (me simbole te Wik-it ende nuk mundem)
Shënimi i pasqyrimit si formulë matematikore

$f(x)=2x , xin mathbb{N}$

Funksioni invers

Nëse për pasqyrimin $f: A to B$ vlen që ç´do $y$ element i $B$ dhe ekziston një elementë $x$ i tillë që :

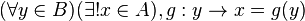
$( forall y in B)( exists !x in A), g:y to x=g(y)$

atëherë themi se kemi të bëjmë me pasqyrimin invers $g$ të pasqyrimit $f$ .
Pasqyrimi invers ekziston vetëm për pasqyrimet bijektive.
Shënimi i pasqyrimit invers $f$ zakonisht shënohet si : $f -$ Për pasqyrimin $f$ themi se është kodomen i domenit $f -$ dhe në të njëjtën kohë domeni $f$ është kodomen i $f -$ .
Figura:

Shumëzimi i funksioneve

Me shumëzimin e pasqyrimeve nënkuptojmë, shumëzimin e dy e më tepër pasqyrimeve (funksioneve), ku elementit $x$ të bashkësisë $A$ i përgjigjet (ekziston së paku një) element $y$ i bashkësisë $B$ , i tillë që në bashkësinë $C$ ekziston së paku një element $z$ i cili i përgjigjet $y$ .Në gjuhen matematikore kjo duket si :

$( forall x in A)( exists !z in C)(g circ f): x to z=g{f(x)}.$

Veprimet binare

Veprim binarë në matematik quhet pasqyrimi f në bashkësinë jo të zbrazët, i tillë që:

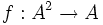
$f: A^2 to A$

Ligjet e veprimeve binare

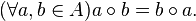
ligji komutativ është nëse vlen: $( forall a , b in A) a circ b= b circ a.$
ligji asociativ është nëse vlen: $( forall a , b , c in A)( a circ b) circ c=a circ (b circ c).$
ligji distributiv është nëse vlen: $( forall a , b , c in A) a circ (b * c)=(a circ b)* (a circ c).$

Nëse në bashkësinë jo të zbrazët $A$ është i përkufizuar veprimi binar $circ$ atëherë për $(A, circ)$ themi se është grupoid.
Po që se veprimi binarë $circ$ grupoidit $(A, circ)$ është asociativ, atëherë për të themi se është semigrup
Nëse në bashkësinë jo të zbrazët $A$ ekziston një element $e$ me vetin:

$( forall a in A)a circ e=e circ a=a$ ,atëherë për $e$ themi se është element neutral.

Grupet dhe nëngrupet

Teoria e grupeve, e lindur ne shekullin 19 si disipline matematike, është nje paraprires i matematikes moderne, sepse ndane perfaqesuesin (p.sh. numrat reale) nga struktura e brendeshme (ligjet e llogaritjes ne grupe).

Punime te medha për teoriene e grupeve vijne nder te tjere nga Evariste Galois, Niels Henrik Abel, Sophus Lie.

Unaza,Trupi dhe Fusha

Unaza

Unazë është bashkësia jo e zbrazët që ka të përkufizua veprimet binare të mbledhjes dhe shumëzimit, ku

$(A, oplus )$ është grup abelian,
$(A, otimes )$ është grupoid dhe
shumëzimi është distributiv ndaj mbledhjes.

Trupi

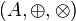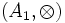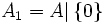Trup quhet unaza asociative $(A, oplus , otimes )$ nëse $(A_1, otimes )$ është grup, ku $A_1 = A| left { 0 right }$ .

Fusha

Fushë quhet trupi 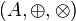$(A, oplus , otimes )$ nëse shumëzimi është kumutativ.