Teoria e gjasës

Teoria e gjasës është degë e matematikës e cila studion fenomenet e rastësishme ^[1]. Koncepte themelore të teorisë së gjasës janë ndryshorja e rastësishme, proceset stohastike dhe ngjarjet e rastësishme: Për shembull hedhja e një kubi për lojë të numëruar me pika në secilën nga gjashtë faqet e tij është një ngjarje e rastësishme. Nëse hedhja e kubit përsëritet një numër të madh herësh do të shohim se këto ngjarje do të plotësojnë një rregullshmëri të caktuar statistikore të cilat mund të studiohen dhe të parashikohen. Teorema të rëndësishme në teorinë e gjasës janë "Ligji i numrave të mëdhenj"" dhe "Teorema qendrore kufitare".

Teoria e gjasës është bazë matematikore e statistikës, ajo ka zbatim të madh në analizën kuantitative të bashkësive të cilat përmbajnë një numër të madh të dhënash, metodat e saj kanë mundësuar zbulimin e fenomeneve fizike në nivelin e atomit që i përshkruan mekanika kuantike.

Historia

Teoria e gjasës i ka rrënjët në analizën e lojrave të fatit përpjekjet e para në këtë drejtim i kanë bërë Gerolamo Cardano në shekullin XVI pastaj Pierre de Fermat dhe Blaise Pascal në shekullin XVII.

Në fillimet e saj teoria e gjasës kryesisht kishte karakter diskret dhe kombinatorik. Teoria moderne e gjasës u themelua nga matematikani i shquar rus Andrey Nikolaevich Kolmogorov. Kolmogorovi e vendosi në baza të forta teorinë e gjasës sepse ai formuloi një sistem aksiomash në vitin 1933.^[2]

Përkufizimi i gjasës

Përkufizimi klasik

Gjasë e një ngjarjeje të rastësishme është herësi i numrit të ngjarjeve të favorshme dhe numrit të përgjithshëm të paraqitjeve të asaj ngjarje me supozim se të gjitha ngjarjet e mundshme kanë gjasë të njëjtë të paraqitjes në fushën elementare të ngjarjeve.

Për shembull ngjarja "Paraqitja e një numri çift pikash gjatë hedhjes së kubit", gjasa e kësaj ngjarje është dhënë me $tfrac{3}{6}=tfrac{1}{2}$ , sepse vetëm tre nga gjashtë faqet e kubit kanë numër çift pikash.

Përkufizimi modern

Le të jetë dhënë bashkësia të cilën e quajmë Fushë elementare e ngjarjeve, e cila i përmban të gjitha ngjarjet e mundshëm gjatë realizimit të një eksperimenti, këtë bashkësi e shënojmë me 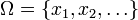$Omega=left { x_1,x_2,dotsright }$ . Supozojmë se çdo element nga 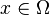$x in Omega,$ , ka një ,,gjasë,, të caktuar të paraqitjes $f(x),$ dhe i plotëson vetitë :

$f(x)in[0,1]mbox{ per të gjitha }xin Omega,;$
$sum_{xin Omega} f(x) = 1,.$

funksioni i gjasës f(x) është një numër real i cili ndodhet ndërmjet 0 dhe 1 për vlera të x nga Ω, dhe shuma e të gjitha f(x) për të gjitha x nga Ω është e barabartë me 1. Ngjarje e rastësishme quhet çdo nën bashkësi 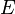$E,$ nga $Om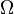ega,$ .

Gjasë e ngjarjes 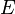$E,$ është numri

$P(E)=sum_{xin E} f(x),.$

Gjasa e ngjarjes së sigurte është 1, dhe gjasa e ngjarjes se pamundshme është 0.